Geocentric Datum of Australia (GDA)
Introduction
Australia has changed the way it references geographic positions on its maps
to accord with a the global coordinate reference system that is directly
compatable with the Global Positioning System (GPS). This page looks at what a
datum change actually means and why we have adopted a new datum. In order to
fully understand the changes, it is necessary to first look at the concepts
behind the geographic positions of features on a map including coordinate
systems and projections.
[back to top]
What is a Coordinate System?
For map reading purposes, an infinite combination of lines can be used to
divide Australia up into equal portions. A common example of a division of this
kind is the local street directory. Street directories use sets of evenly spaced
lines, known as a coordinate system, to break large areas of land into parcels.
By giving each portion a reference marker in the north-south and east-west
direction as well as a unique page number, features in the directory can be
identified more efficiently as the area in which the feature exists is much
smaller.
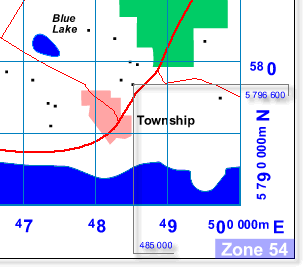
Street Directory Reference System
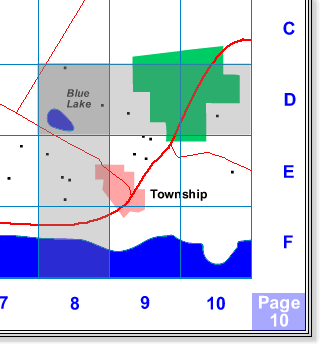 |
In the above map, the Blue Lake is located by the
reference Page 10, D8. This kind of system is used in street
directories and defines only the grid square in which the feature
exists. Though the coordinate system is repeated on each page, by
specifying the page number each grid is uniquely identified.
|
Topographic Map Reference System
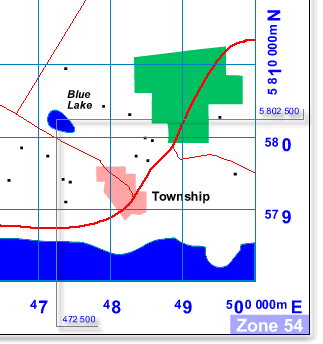 |
In the above map, the Blue Lake is located by the
reference 472 500E, 5 802 500N. Though the system is more complex
it allows features to be located more exactly by interpolating
coordinate values in both directions. Like a street directory, the
coordinate system is repeated but instead of on each page, it is only
between zones.
|
Feature referencing on Geoscience Australia's mapping products work on a
similar principle to a street directory but there are two main differences:
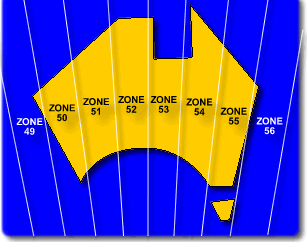
- Geoscience Australia's mapping products do not use page numbers to divide
the country into portions. Instead, maps are divided into zones. Zones cover
a much larger area than a single page in a Street Directory and are numbered
according to a world wide convention. Australia is covered by zones 49 to
56, each zone covers 6 degrees of longitude. Zones are related to the
Universal Transverse Mercator projectionand used
by many countries to map the earth.
- The coordinate system used on Geoscience Australia's mapping products
enables features to be pinpointed to a greater degree of accuracy than a
Street Directory where a grid area, in which the feature exists, is defined
rather than the feature itself. Street directories generally use a letter
and a number, topotgraphic maps use a consecutive range of numbers in both
directions. The range of numbers, allows the position of features to be
interpolated to much greater degree of accuracy.
[back to top]
Cartesian Coordinates, Grid Values X and Y
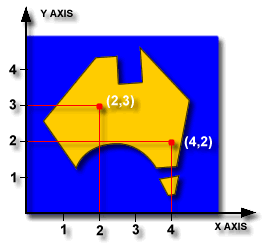
The type of coordinates found in a street directory and on Geoscience
Australia's topographic maps are known as Cartesian Coordinates. Cartesian
Coordinates are related to a line that represents zero in the east-west
direction, known as the X axis, and a line that represents zero in the
north-south direction, known as the Y axis.
Movements by a point away from the axes are recorded as a set of two values,
known as coordinates. Coordinates tell you how far away from the origin of the
axes, 0 on X and 0 on Y, that you are. By convention, the point's position is
identified by quoting the distance along the X axis first, and distance along
the Y axis second, thus each point has a unique name.
These are the mathematical coordinates you find on a map. In cartography and
surveying, the X axis coordinates are known as Eastings, and the Y axis
coordinates as Northings.
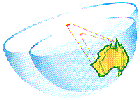
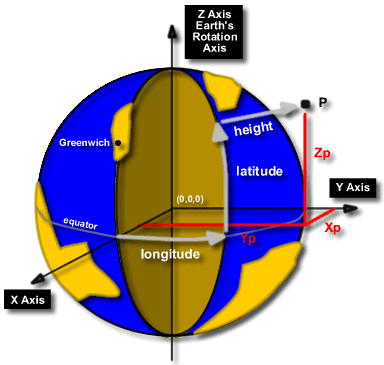
Local 3D Cartesian Coordinates, Grid Values X and Y + Height Z
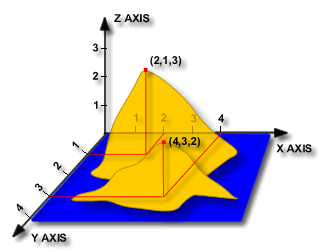
Cartesian Coordinates can define a point in space, that is, in three
dimensions. To do this, another axis must be introduced. This axis will
represent a height above the surface defined by the x and y axes. This new axis
is known as the Z axis. For local 3D cartesian coordinate systems, the Z axis
represents "up".
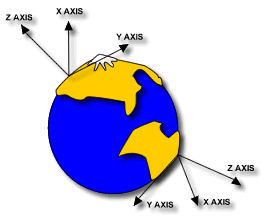
This diagram shows the earth with two local coordinate systems defined on
either side of the earth. The Z axis points directly up into the sky.
These coordinates are read like the 2D Cartesian System only there is now an
extra coordinate in the direction of z; instead of (X,Y) it is (X,Y,Z).
[back to top]
Cartesian Coordinate Systems in Australia
The new cartesian coordinate system that will be used in Australia will be
known as the Map Grid of Australia 1994 (MGA94).The cartesian system that is
being phased out is called the Australian Map Grid, there are two versions of
the coordinates from this system, the originals from 1966 and their subsequent
update in 1984. For the purposes of this document they will be considered as the
same (they differ only by a few metres) and will be refered to as the AMG66/84.
Where street directory coordinates are arbitrary, the values assigned in
Geoscience Australia's maps are derived from the position's longitude and
latitude. Longitude and latitude are coordinates that relate to the feature's
positions on the spherical earth.
[back to top]
Geographic Coordinates - Longitude and Latitude
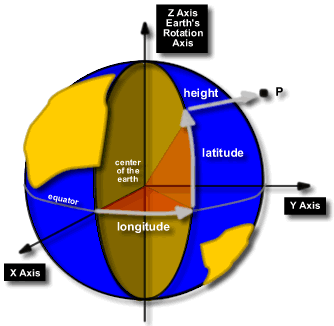
Lines of longitude intersect both the North and South poles. They are
numbered using degrees beginning at the Royal Greenwich Observatory in England,
which is designated as 0°, and continue both East and West until they meet at
180°.
Lines of latitude are measured as an angle from the equator (0°) to either
Pole, 90° South and 90° North. The equator is a line of latitude.
Latitude and longitude are collectively known as geographic coordinates.
As with cartesian coordinates, one point on the earth can have many different
geographic coordinates assigned to it, depending on how the reference system was
defined. The GDA94 will have longitude and latitude values that relate to a
reference surface called the Geodetic Reference System 1980 [GRS80].
So any point on the earth's surface can have a set of geographic coordinates
and a corresponding set of cartesian coordinates. The next section explains how
the two are related.
[back to top]
Projections
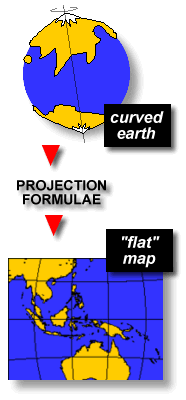
World globes are a good estimation of the earth's surface but their scale is
too small to allow you to plan trips across town. A flat map of the region that
we can fold up and put in our pocket is more functional.
To convert the round earth to flat map is complicated. The best way to
illustrate the difficulty in doing this is by thinking of the earth as a rubber
ball with the land and water painted on it. To flatten the rubber ball into a
flat square we need to cut it up and stretch it.
Because the rubber ball is being stretched, the land shown on it will be
distorted from its original shape.
This same, cutting and stretching process is used to make maps through
mathematical formulae called 'Projections'. Projection formulae take the
geographic coordinates from the spherical earth (longitude and latitude) and
convert them to cartesian coordinates (X & Y).
There are many projection formulae that can be used and consequently maps can
look very different.
A 'Universal Transverse Mercator' (UTM) projection of the GDA94 geographic
coordinates produces cartesian coordinates known as Map Grid of Australia 1994
(MGA94). This UTM projection was also used for the Australian Map Grid, 1966 and
1984 [AMG66/84] - the coordinate system of maps that are being superceeded by
the MGA94.
You may wonder why the AMG66/84 and MGA94 are different if they are both
projections of geographic coordinates to cartesian coordinates. It is because
the geographic coordinates are different. The AMG66/84 cartesian coordinates are
based on the geographic coordinates derived from the Australian National
Spheroid [ANS] and the MGA94 cartesian coordinates come from the geographic
coordinates defined by the Geodetic Reference System 1980 [GRS80]. They are from
different models of the earth, more about this next section.
[back to top]
Mathematical Figures of the Earth
The shape of the earth has always been speculated upon - historical accounts
of sailors record that they feared falling off the edge of the earth if they
sailed too far. The concept of a flat earth was eventually disregarded and the
earth was thought to be perfectly spherical until Issac Newton conducted studies
in the late 1600s.
Issac Newton contended that his theory of gravity would mean that the earth
would not be perfectly spherical but slight squashed at the poles and bulging at
the equator due to the forces acting upon it as it span. This theory was proven
and today, it is accepted that the earth is actually slightly elliptical in
shape.
Because the earth's surface is very complex, its shape is simflified so that
distances can be indirectly determined using mathematical equations. Modelling
the shape of the earth as accurately as possible is vital for geodesists who
make very precise calcuations on its surface over long distances. For most
practical purposes, estimating the shape of the earth using a sphere is accurate
enough over relatively short distances.
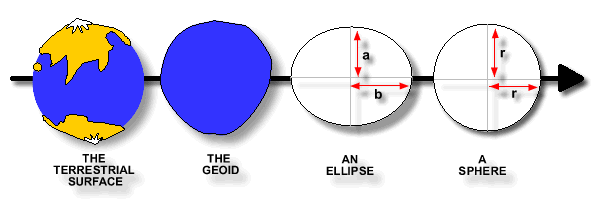
| The terrestrial surface refers to the earth's
topography. It is very complex with mountain ranges and oceans and it is
the surface upon which we live and measure. Because the earth is not
even, it is not suitable for exact mathematical computations. |
The first simplification estimates the
earth's surface using mean sea level of the ocean with all continents
are removed - this surface is called the Geoid. Due to variations in the
earth's mass distribution (oceans and land), the Geoid has an irregular
shape that is described as "undulating". It is an equipotential
surface. This means that potential gravity is the same at every point on
its surface. |
Measurements have shown that the earth is in
fact slightly "squashed" at the poles and bulges at the
equator due to forces acting upon whilst it spins. Mathematically this
shape is described as an ellipsoid of revolution, an oval that revolves
about its shortest dimension. It is a mathematical approximation of the
Geoid. This shape is used for exact measurements over long distances,
across continents or oceans. |
The ellipsoid can be further simplified into
a sphere. To define a sphere, only the radius is required. The radius
often used when modeling the earth as a sphere is 6371 000 meters. This
shape is a close approximation of the earth's shape and is a suitable
approximation for most applications.
|
[back to top]
Ellipsoids Used in Australia
Some earth models relevant to Australia are the World Geodetic System 1984
[WGS84] and the Geodetic Reference System 1980 [GRS80]. The WGS84 is used for
the Global Positioning System and is very similar to the GRS80. They have a
small difference in the definition of their ellipsoid parameters and generally
may be treated as the same.
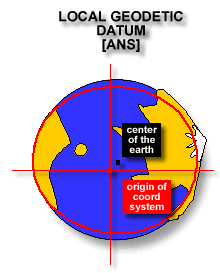
The GRS80 (and hence the WGS84) is a geocentric system. This means that the
origin of its coordinate systems corresponds with the centre of mass of the
earth.The GRS80 is important to Australia as it is the ellipsoid used to define
the GDA94.
The Australian Map Grid [AMG66/84], the system being updated, was based on
the Australian National Spheroid [ANS] which was an ellipsoid designed to be the
best estimate of the earth's shape around the Australian continent rather than
the world. As a result, the origin of the ellipsoid used in its definition did
not correspond with the centre of the earth - it was about 200m away from it.
Consequently the shift to the new datum will mean that all coordinates will
shift by approximately 200m to the north east.The width of an ellipsoid at the
equator is called the semi major axis and is conventionally named the letter
'a'. The flattening of the ellipsoid is refered to by the letter 'f' and is a
measure of how much the ellipsoid differs from a sphere.
| Ellipsoid |
Symbol |
ANS |
GRS80 |
| Semi major axis |
a |
6378160.0 metres |
6378137.00 metres |
| Flattening |
f |
0.003352892 |
0.003352811 |
The Map Grid of Australia MGA94, the new system, uses the GRS80 ellipsoid. It
was designed to be a best estimate of the earth's shape globally. Its centre
corresponds with the centre of the earth.
[back to top]
What is a Datum?
A datum is a framework that enables us to define coordinate systems. The
framework includes the ellipsoid and other parameters not discussed here, for
information about these see the ICSM
GDA Home Page.The way a datum is defined has changed with the improvement of
measurment techniques through technology. The AGD66/84 was defined
differently to the GDA94, the two methods are outlined briefly below.
Traditional Geodetic Datums - The AGD66/84
To describe positions on the earth accurately,
traditionally two datums were required; a horizontal datum and a
vertical datum.
|
Vertical Datum
A Vertical Datum is used to fix a position in the vertical
direction, up and down the Z axis.
A vertical datum is a line, value or set of values from which heights
are measured. Australia's vertical datum is the Australian Height Datum
[AHD] which approximates mean sea level and was determined by monitoring
tide gauges around the Australian coastline. The change of horizontal
datum to the GDA94 will NOT affect height the currently used
Vertical Datum.
|
Horizontal Datum
A horizontal datum is used to fix a position in the X and Y directions.
A horizontal Datum was traditionally defined using an ellipsoid and an
origin. The ellipsoid was generally choosen for a best fit of the geoid
locally.
The origin of the AGD66/84 is the Johnston Geodetic Station. More
information about this datum can be found at the GDA
Homepage
|
[back to top]
Modern Geodetic Datums - GDA94
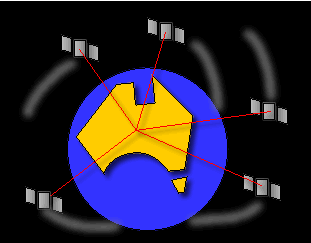
Today's technology means that a new datum can be based on several well
determined points. The 8 points used to define the GDA94 are known as the
Australian Fiducial Network [AFN]. The adopted coordinates of the AFN were
computed in terms of the International Terrestrial Reference Frame (ITRF) and
from these AFN coordinates the geodetic network that covers the whole continent
was recomputed. The ITRF is based on a number of very accurate observations all
over the earth, including Very Long Baseline Interferometry (VLBI), Satellite
Laser Ranging (SLR), Lunar Laser Ranging (LLR) and the Global Positioning Sytem
(GPS)"
The measurements relate to a 3D earth-centered cartesian coordinate system,
shown above. This system could be considered a 'global' 3D cartesian coordinate
system in contrast to the 2D system previously
described.
Though the AFN provides coordinates in three dimensions, only the horizontal
components have been adopted. Heights in Australia remain those of the AHD.
[back to top]
Why did we change to a Geocentric Datum?
The main reason was so that we can use the Global Positioning System [GPS]
more easily. The Global Positioning System is becoming more and more widely used
for navigation by both the spatial sciences and the general public world-wide.
Geocentric datums have been adopted for most aeronautical and shipping
applications due to its international capabilities. As GPS is based on a
geocentric datum, to use the coordinates here in Australia means we have to
convert the coordinates to our datum, the AGD66/84. With the introduction of the
GDA94, the datums will both be based on the same ellipsoid and this will
eliminate the need for a complex conversion as the coordinates read from the GPS
will be the same as those of the GDA94.
For further Technical Knowledge on this topic, visit the ICSM
GDA Home Page For information on what stage Geoscience Australia is at Geoscience
Australia GDA Implementation Statement
This page was copied from
http://www.auslig.gov.au/geodesy/datums/ on the 19/12/02